10. LLaDA: Large Language Diffusion Models
A new paradigm for LLMs is emerging, will it last and scale?
Introduction
Diffusion models excel at generative tasks where adding Gaussian noise to a clean sample leads to a gradual degradation process that can be smoothly reversed. This is the case for images, videos, audio, and molecules, where the underlying data exists in a continuous space, and adding noise does not completely destroy its structure.
However, this approach does not naturally extend to text. Since language is inherently discrete, there is no such thing as a noisy word. For instance, randomly replacing words or characters would quickly produce meaningless sequences rather than a recoverable intermediate state.
Today, we’ll take a look at the paper Large Language Diffusion Models [1], a very recent approach that rethinks how diffusion can be applied to discrete text data and challenges established autoregressive architectures.
Method
As in conventional diffusion models (which I discussed in a previous post), the method defines a model distribution through a forward process that corrupts the data and a reverse process that reconstructs it and later generates it from scratch. This contrasts with autoregressive LLMs, which rely on the next-token prediction formulation to define the model distribution.
However, since text is discrete, LLaDA (Large Language Diffusion with mAsking) replaces the traditional noise-based corruption with discrete random masking in the forward process and trains a mask predictor to approximate its reverse process. In all that follows, tokens are created from the corpus using a standard tokenizer vocabulary.
➡️ Forward process: masking instead of noising
In standard diffusion models, controlled corruption occurs over multiple timesteps, which we can equivalently rescale as a time in the interval [0,1]. At time t=0, the data sample is clean, at time t=1, it is completely corrupted and approximates pure noise. This process is modeled as a Markov chain, meaning each state depends only on the previous one.
LLaDA adopts a similar approach using masking. For any time t in [0,1], each token in the sequence is masked independently with probability t or remains unmasked with the complementary probability 1−t. This means, at t=0 the sequence is untouched, and at t=1 all tokens are masked. Since each state is sampled independently from the original sequence and depends only on the time t, by design the forward process is non-Markovian.

Overall, this remains straightforward to sample from the initial clean state, which is all we care about for efficient training.
⬅️ Reverse process: predicting the masked tokens
Given a partially masked text corresponding to a timestep t, the reverse process reconstructs the original word sequence. Instead of denoising in a continuous space, LLaDA directly predicts the masked tokens using a vanilla bidirectional transformer trained with cross-entropy loss.
This is similar to the masked language modeling pretraining task of BERT [2], but the masking ratio is not fixed and varies across training examples, ranging from fully masked to completely unmasked sequences, depending on the value of t. The linear masking probability here is similar to having a noise schedule in continuous diffusion models and ensures that the model sees corrupted data at all stages.
Notably, the transformer model must learn representations that work regardless of the number of masked tokens, as the timestep is not explicitly provided as input. However, it can be internally inferred since the number of masked tokens is approximately Lt, where L is the sequence length.

This masked pretraining process uses a fixed sequence length of 4096 tokens, but to enhance the ability of LLaDA to handle variable-length data, 1% of the sequences are set to a random size, uniformly sampled from the range [1,4096]. Training of the 8B-parameter transformer is done on 2.3 trillion tokens comprising general text, high-quality code, math, and multilingual data.
SFT and generation at inference time
After masked pretraining, the model goes through a round of supervised fine-tuning (SFT) on 4.5 million pairs of prompts and responses to enhance its ability to follow instructions. This phase is identical to pretraining, except that the prompt is left unchanged and masked tokens appear only in the response portion of the data.
A dynamic sequence length is employed during SFT, but short sequences are padded with end-of-generation tokens |EOS| within each mini-batch. It is in this phase that the model learns to control the length of its responses, as the |EOS| tokens are treated and masked as any other token.
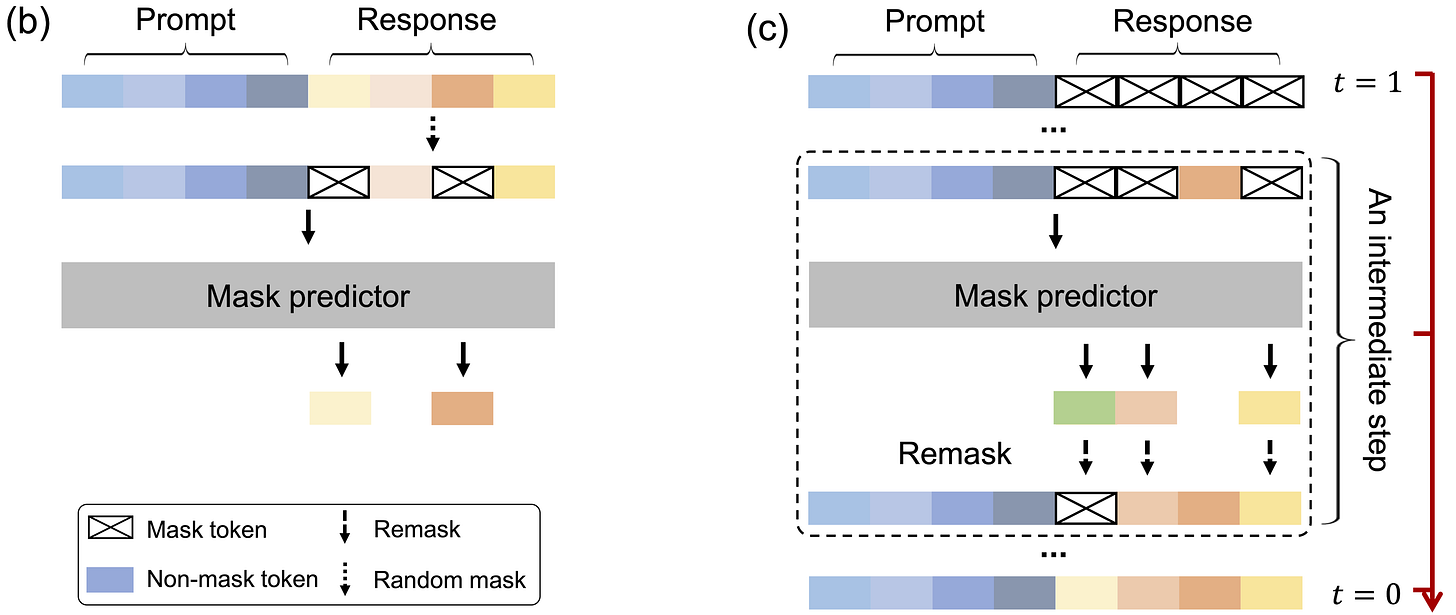
How to do inference is interesting, as we need to simulate intermediates and refine them. The total number of sampling steps is a hyperparameter, which naturally provides LLaDA with a trade-off between efficiency and sample quality. Uniformly distributed timesteps are employed by default, which means the number of masked tokens decreases linearly step by step.
We start with the user prompt and a fully masked response. After sending the sequence into the mask predictor and predicting all masked tokens simultaneously, there is a first response candidate. Subsequently, we remask a portion of the predicted tokens to obtain, in expectation, a masked sample aligned with the next timestep, ensuring that the transition of the reverse process aligns with the forward process for accurate sampling.
In principle, the remasking strategy should be purely random. However, the authors explore a strategy called low-confidence remasking, where the lowest confidence tokens based on the prediction logits are chosen. Intuitively, it makes sense as the least confident parts should not be set in stone from the beginning.
Another option that can be performed at inference time is semi-autoregressive remasking, which is a hybrid between diffusion and classic autoregressive models. First, the response is chunked into several blocks, which will be generated from left to right. However, within each block, we apply the reverse process to perform sampling using diffusion with low-confidence remasking. This boosts the performance of the instruction-tuned model.

Conclusions
LLaDA presents evidence that diffusion-based models for text can be a viable alternative to traditional autoregressive ones. At the scale analyzed in the paper (8B parameters and 2.3T training tokens), the model surpasses LLaMA2 7B (trained on 2T tokens) on nearly all tasks and is overall competitive with LLaMA3 8B (trained on 15T tokens).
While it is unclear what happens at a larger scale, there are already hints that using a bidirectional diffusion-based model can provide better responses in tasks like math, coding, and reversal reasoning, since the model can easily fix errors and improve answers quickly. Imagine coding an entire program only to realize you forgot to initialize that variable at the beginning, and you cannot go back…
Overall, we live in an exciting time as the prevailing assumption that key LLM capabilities are inherently tied to an autoregressive formulation is being challenged. Just last week, a new company named Inception [3], co-founded by Stanford computer science professor Stefano Ermon, one of the leading experts in diffusion models, emerged from stealth with a new diffusion-based LLM for coding.
We’ll see in a few months where this leads, but for now, enjoy the most satisfying code generation video you have ever seen, credits to Inception.
References
[1] Large Language Diffusion Models
[2] BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding
[3] Inception



