Introduction
Transformers have undeniably taken the world of machine learning by storm, becoming the gold standard in natural language processing after the release of the iconic Attention Is All You Need paper [1]. Designed as general-purpose models, their impact quickly surpassed language, reshaping how we approach sequential modeling in domains like audio, video, and genomics. And if something isn’t inherently sequential, take for example images, Vision Transformers (ViTs) [2] demonstrate that it can probably be adapted to work with a transformer with minimal adjustments.
This game-changing architecture is usually presented with the famous illustration from [1], where the narrative tends to highlight the multi-head attention mechanism, layer normalization, and MLPs more than the skip connections.
Given this, it’s almost instinctive to perceive transformers as a simple stack of layers at first glance — a sequential composition of identical and independent blocks, connected with residual paths to facilitate end-to-end training. However, skip connections play a far more profound and geometric role in transformers, setting them apart from their ResNet counterparts. To understand why, let’s first introduce the concept of the residual stream, a topic I found particularly fascinating when first reading [3].
Identity as a communication channel
Skip connections perform identity mapping and introduce neither extra parameters nor computational complexity. These shortcuts can be seen as a persistent flow of information from the input to the output, which layers update through their computations. All it takes is a shift in perspective from the left view to the right one when considering the same sequence of operations. The identity path in the right diagram (and the left, of course) is what we depict as the residual stream.
The residual stream not only facilitates backpropagation but also serves as a mechanism for preserving features from earlier stages. Layers read from the stream and write back to it, enabling progressive refinement. That is the essence of [4], arguably a monster of a contribution, cited over 250.000 times at the time of writing. However, not all residual streams are created equal.
The purpose of residual paths
In the case of ResNets, the dimensionality of the residual path changes between layers due to the down-sampling, with the number of dimensions progressively increasing (e.g. 64 to 512) while the size of the image input decreases. In the plot that follows, the dotted lines indicate sharp transitions in how features are represented: at one stage, the intermediate image embeddings reside in an N-dimensional space, and immediately after, they expand into a 2N-dimensional one.
On these boundaries, the balance between the write term from the block and the memory contribution from the residual stream undergoes a significant shift. What enters the network and what we get at the end are hard to relate.
On the other side, in transformers, the residual stream maintains a constant dimension equal to the embedding size from start to finish. Everything shares the same representational space, enabling the residual stream to function as persistent storage while each layer proposes gradual updates. Imagine a point cloud entering this very high-dimensional space, and a transformed point cloud — enriched, moved, and contextualized — exiting from the same.

One fascinating aspect is that the residual stream in transformers has a deeply linear structure. Every layer performs an arbitrary linear transformation to read information from the stream and then performs another arbitrary linear transformation to write its output back into it. Therefore, the representation space doesn't have a privileged basis and we could rotate all the matrices interacting with it, without changing the model behavior at all [3].
Geometry in action
Now, each component has a different way of altering the journey of the point cloud, and cool geometry is involved under the hood:
The attention mechanism is where information is shared between different tokens. The high-dimensional representations talk to each other in this stage, emphasizing contextual relationships and global dependencies. Notably, attention heads operate on a relatively small subspace compared to the embedding size, and they can very easily write their computations to completely disjoint subspaces of the residual stream and not interact with each other.
MLPs, on the other hand, act as knowledge banks and local feature refiners, focusing on elaborating individual token representations. They account for the majority of the parameters in a transformer. Since MLPs are wider in the middle (typically by a factor of four), each token is temporarily projected into an even larger space where information is organized and accessed along specific directions (or most likely, a superposition of dimensions [5]), before being projected down to the stream dimension.
Layer normalization is also quite fascinating in its geometric interpretation. In an embedding space with D dimensions, it involves three steps: first, projecting points onto the hyperplane perpendicular to (1, 1, …, 1); second, normalizing the projection so that it lies on the surface of a (D-1)-dimensional hypersphere with radius √D; and finally, applying learned scaling factors along the axes, transforming the hypersphere into an ellipsoid.
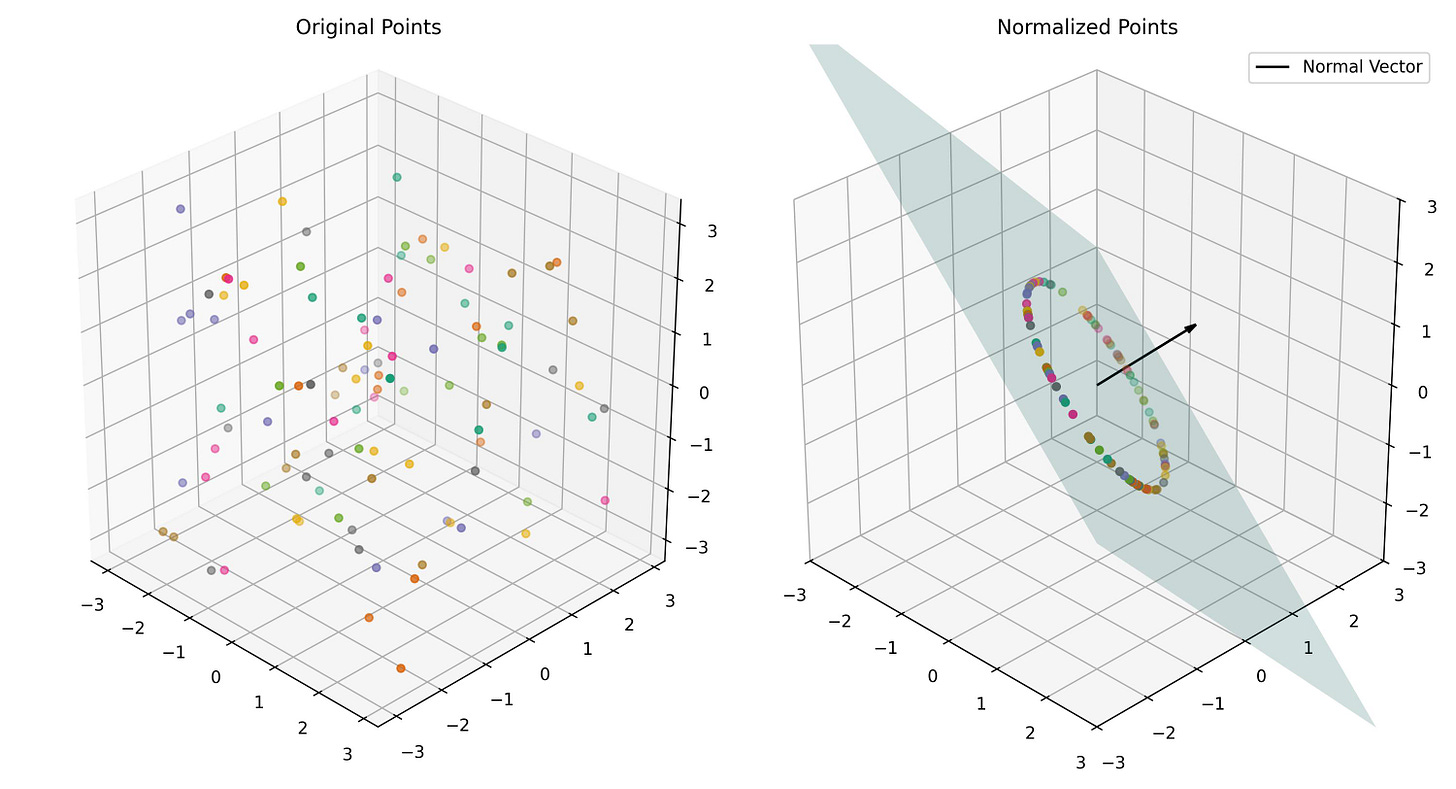
Layer normalization applied to 3D data places points on the surface of a 2D ellipse perpendicular to (1, 1, 1). While this operation does not yield information gain, it ensures embeddings stay organized on a common surface, keeping their magnitudes consistent.
Conclusions
Sometimes, a simple change in perspective can reveal fresh insights into why something works so effectively. Viewing the input, intermediates, and output as an evolving point cloud within the same space offers a glimpse into the inner workings of a transformer. Whether encoder-only, decoder-only, or the full encoder-decoder variant, there is always a way to view them operating within this framework as dynamical systems.
And you, were you thinking of this architecture as just a mere stack of layers and never looked at the residual path that way? I hope it’s now a completely different story. I recommend watching some amazing 3B1B videos on transformers [5] for more mind-blowing facts and to fully grasp the geometry under the hood. See you next week!
References
[2] An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale
[3] A Mathematical Framework for Transformer Circuits






