Introduction
Diederik Kingma and Max Welling received the inaugural ICLR Test of Time Award in 2024 for their groundbreaking work Auto-Encoding Variational Bayes [1], a paper published in 2013.
Over a decade later, Variational Autoencoders (VAEs) have evolved from being standalone generative models to becoming a foundational building block in advanced systems like Stable Diffusion and more [2]. What makes them so special? Let’s find out.
Autoencoders vs VAEs: the difference
A standard autoencoder uses a neural network with a bottleneck layer to reconstruct high-dimensional data in an entirely unsupervised manner, requiring no labels. The architecture consists of two components:
An Encoder, compressing layer after layer the input into a lower-dimensional latent code, capturing only the essential features.
A Decoder, reconstructing the original data from the compressed latent code, with increasingly larger layers to restore the full dimension.
By learning an identity function, this process inherently performs dimensionality reduction. The bottleneck layer captures a compact latent representation suitable for downstream applications, such as search or out-of-distribution detection. However, this is a pointwise mapping from input to latent and vice versa, making the latent space poorly organized.
On the other hand, VAEs introduce a probabilistic framework and enforce structure in the latent space by modeling it as a probability distribution, typically Gaussian. Instead of learning fixed encodings, VAEs learn a latent distribution for each input.
This allows for smooth interpolation between data points and enables the generation of new data by sampling from the latent space, making VAEs effective for generative modeling tasks while preserving the dimensionality reduction capabilities of traditional autoencoders. When consistency is required, the forward pass can be made fully deterministic by using the mode (mean) of the latent distribution. This typically happens after training is complete.
While impressive in their own right, we now have many superior generative model classes like GANs, diffusion models, and flow-matching-based approaches. So, what makes VAEs deserving of the prestigious Test of Time Award? What are the key insights from the original paper, and how have VAEs evolved to find a new purpose?
The VAE recipe for immortality
This elegant work bridges the gap between deep learning and scalable probabilistic inference, establishing a robust framework for generative modeling and representation learning. Three main contributions are the following:
1. Maximizing the evidence lower bound
When training a VAE, the objective is to maximize the likelihood of generating real data. However, modeling latent variables as distributions makes direct optimization of such likelihood intractable, as it involves summing over all possible latent variables.
The evidence lower bound (ELBO) cleverly circumvents this problem by replacing the marginal likelihood with a smooth and easily computable objective function, making the optimization feasible with standard gradient descent. In addition, the ELBO is a true lower bound, guaranteeing no theoretical gap under optimality conditions!
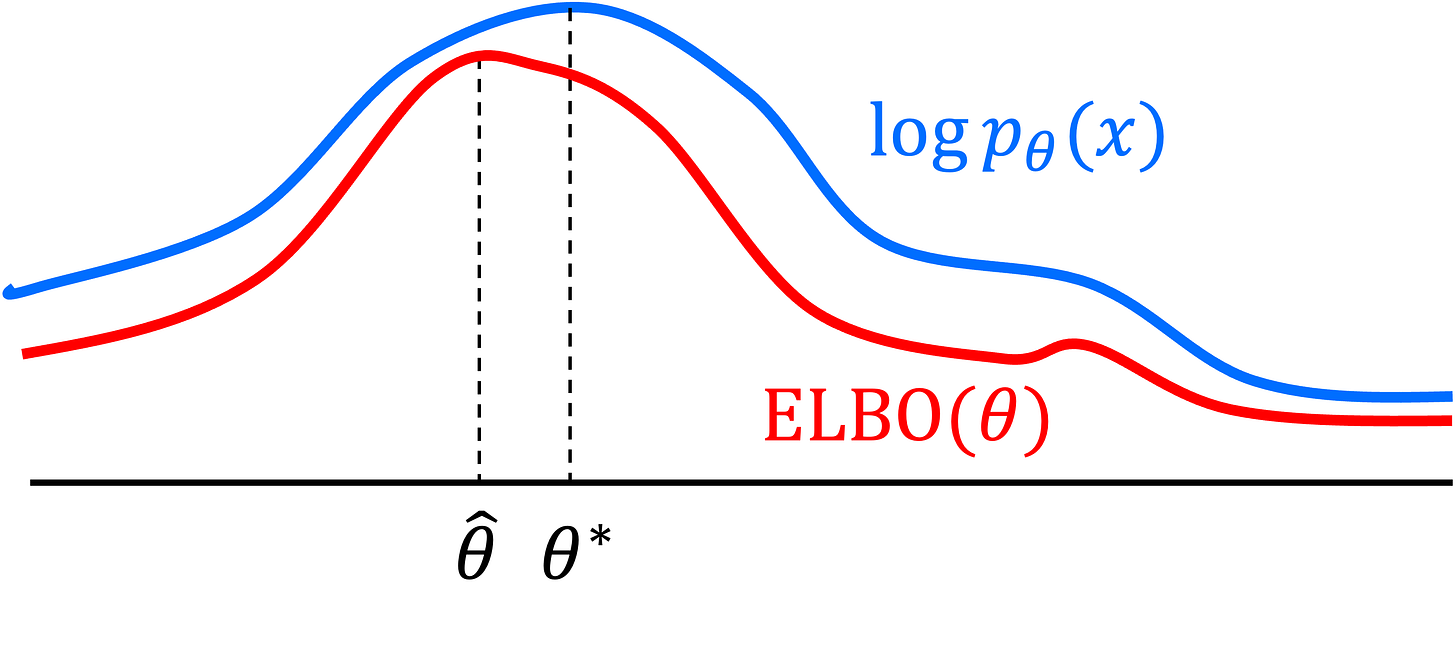
The ELBO objective consists of two parts:
A reconstruction term, ensuring the decoder can accurately recover the input data. Typically, a combination of L1, L2, and perceptual losses is used.
A regularization term, assuring that the latent variables follow a predefined structure, such as aligning with a Gaussian distribution. This is implemented through a KL-divergence term.
Both ingredients can be computed analytically and optimized efficiently, thanks to the next idea introduced in the paper.
2. The reparameterization trick
The reconstruction term in the ELBO requires generating samples from the latent distribution. However, sampling is a stochastic process, which disrupts the flow of gradients and prevents plain backpropagation.
The reparameterization trick addresses this issue by decoupling the stochasticity from the learnable parameters of the model. By expressing a random variable as a deterministic function of model parameters and an auxiliary independent random variable, differentiation can proceed seamlessly.
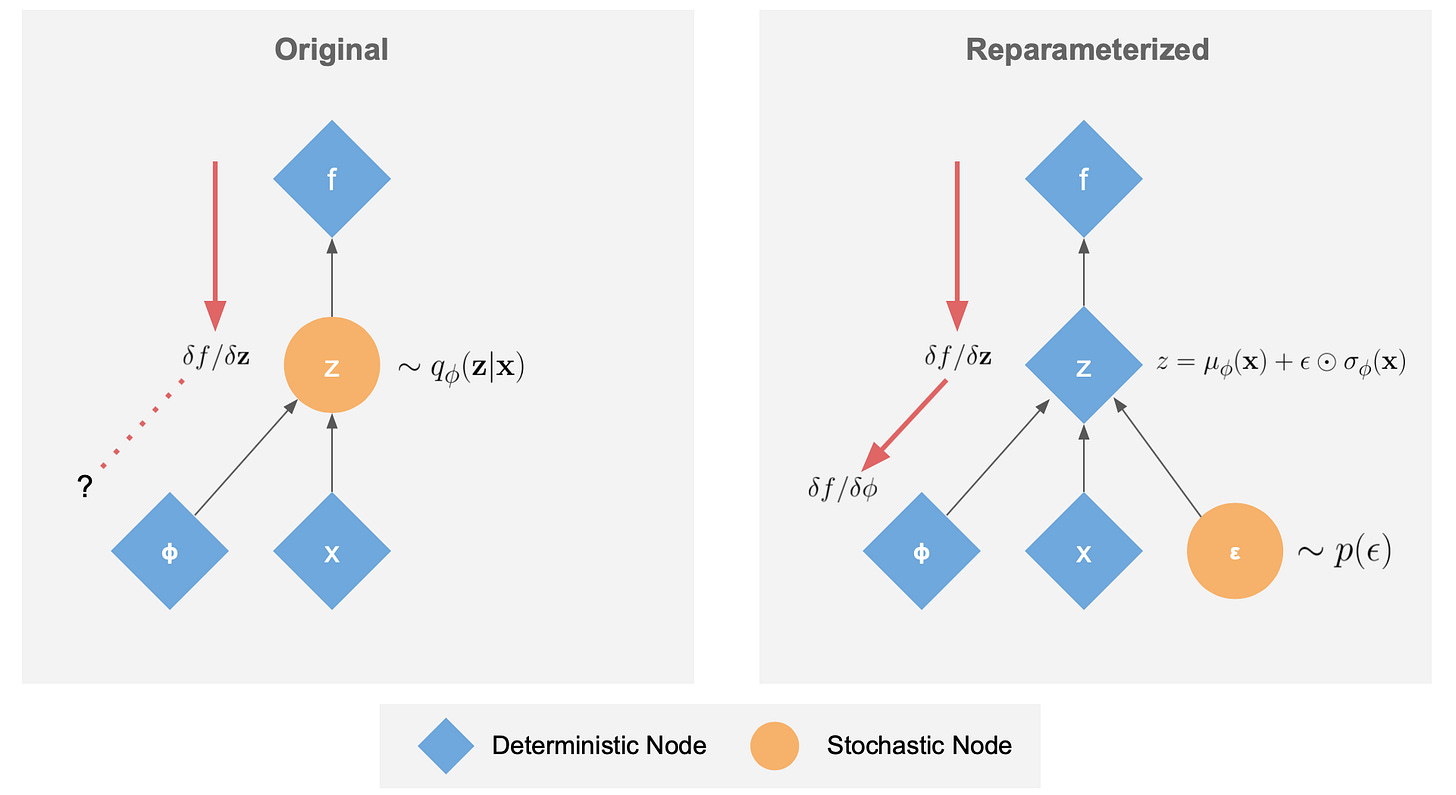
For example, imagine sampling from a Gaussian distribution with a given mean and variance. This is equivalent to starting with a sample from a standard normal distribution (mean 0, variance 1) and then shifting by the desired mean and scaling by the standard deviation. The key advantage of this method is that it separates the randomness from the model parameters, allowing gradients to flow through them during optimization. Sounds very easy at first glance, but as always with some of the greatest ideas in ML, someone had to come up with it!
3. Amortized inference
Before VAEs, traditional variational methods required solving an optimization problem for each data point. VAEs introduced the concept of amortized inference, where a single encoder network learns to approximate the latent distribution for all inputs simultaneously. This significantly reduces computational overhead and makes the framework scalable to large datasets commonly encountered in modern machine learning tasks.
While the same latent variables describe every input, what is different for each data point is our belief about the specific values of these variables. In true Bayesian fashion, these beliefs are updated upon observing the input data, pointing to a more concentrated region of the latent space.
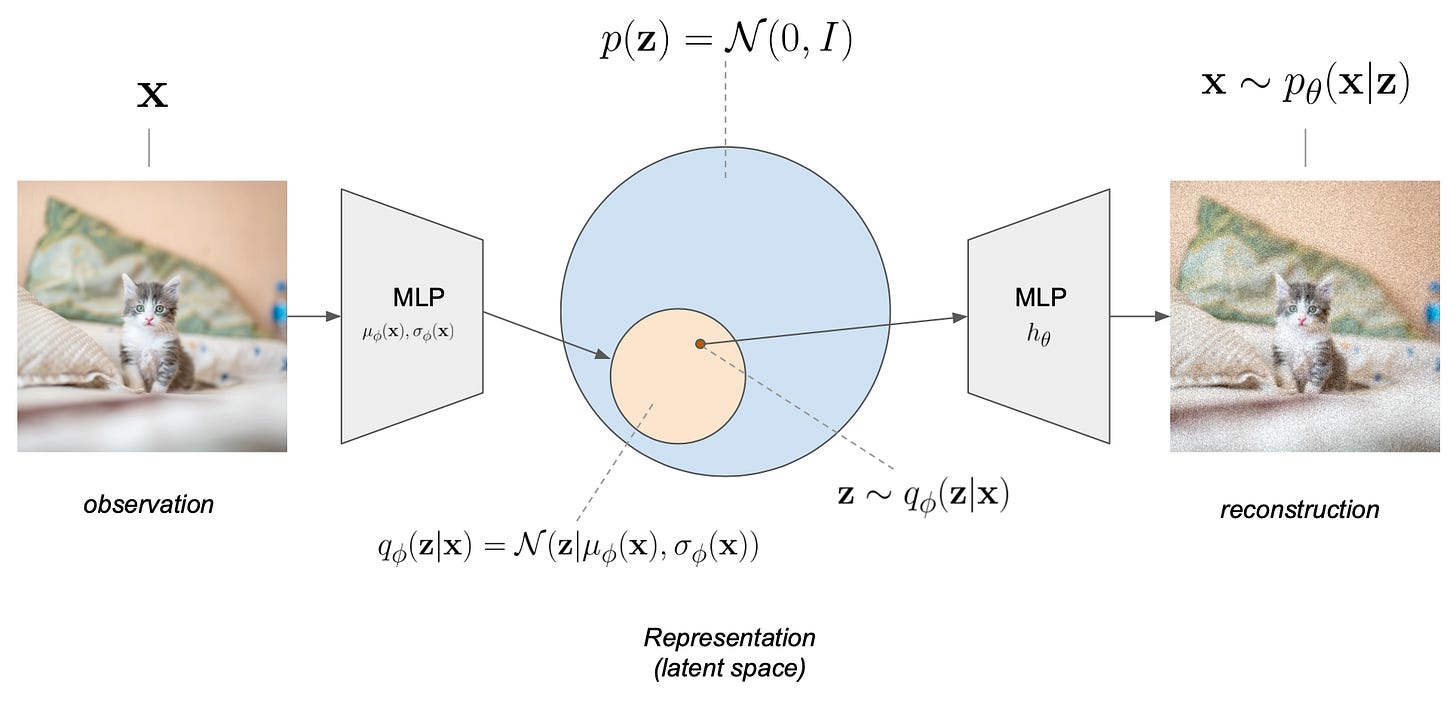
The unsung hero of modern generative systems
The true legacy of VAEs lies in how they have become foundational building blocks for advanced ML systems. A prime example is their role in Stable Diffusion and FLUX, where they create an efficient, smooth, and well-structured latent space in which the generation of new samples happens through a separate process. The fact that the latent representation is meaningful across its entirety is key, as the generation process is unlikely to end up exactly on a training data point.
Research on VAEs is still ongoing: in the case of text-to-image models, the quality of generated images (not the semantic!) remains closely tied to the capacity of the VAE to reconstruct data from the latent space. For example, while keeping all other architecture layers the same, increasing the latent channel size is proven to have a massive impact on reconstructing fine details.

Based on this, recent image generative models have opted to train the VAEs with four times the latent channels (16) compared to the previous generation to achieve superior image quality. And there is likely even more happening behind the scenes with optimized loss functions and other techniques that are not immediately apparent. For example, the VAE in the first version of Stable Diffusion incorporated a discriminative loss during training, similar to what is used in GANs.
Conclusions
VAEs may have started as standalone generative models, but their real brilliance lies in their adaptability. The foundational contributions in [1], such as optimizing the ELBO, the reparameterization trick, and amortized inference, have enabled scalable and efficient representation learning.
As research continues, they will likely keep popping up and proving that great ideas, when built upon, never truly go out of style. Just like learning to compress data: even with more powerful hardware, it never gets old.
If you’re curious about the math or code aspects I haven’t discussed, check out the resources below. I highly recommend reading [3], or watching [7] if you are a visual learner.





